Theorem Assume that and |(f ⁿ)’(p)| < 1. Then there is an open interval such that for every :

Proof: By the assumption , i.e. f has a continuous derivative and is continuous for every xÎ [a,b], where [a,b] is a closed subset of  . Then there exists an e >0 such that |(fⁿ)’(x)|<A<1 for xÎ [p-e ,p+e ]. The theorem is proved by induction, i.e. the theorem is first proved to hold for k=1. By the meanvalue theorem there exists a x , |x -p|<|x-p|, such that:

According to the above f ⁿ(x) is closer to p than x. The induction assumption is now:

The inequality is then proved to hold also for k+1:

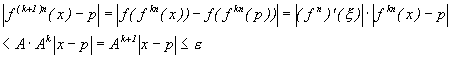
Induction gives that the inequality holds for every k and the following conclusion can be done: f ^kn(x)® p when k® ¥.

Theorem Assume that and |(f ⁿ)’(p)| > 1. Then there is an open interval such that for every xÎU\{p} there exists kÎN such that:

Proof: By the assumption , where [a,b] is a closed subset of  . Then there exists an e >0 such that |(f ⁿ)’(x)|>A>1 for xÎ ]p-e ,p+e [. Take an arbitrary x#p from the interval ]p-e ,p+e [ and do the antithesis that f ^kn(x)Î U for all k. Then the theorem is proved by induction, i.e. the theorem is first proved for k=1. By the meanvalue theorem there exists a x , |x -p|£ |x-p|, such that:

According to the above f ⁿ(x) is further from p than x is from p. The induction assumption is now given by:

The inequality is then proved also to hold for k+1:

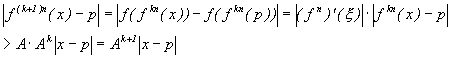
Induction gives that the inequality holds for every k and the conclusion that f ^kn(x)® ¥ when k® ¥ can be made. The antithesis is false, which means that the proof is finished.

The tent map is chaotic on [0,1].

Proof: Consider an arbitrary interval I=[1/2d ,d ], 0<d <1/2. Now there exists a natural number k such that 2^k-1d<1/2<2^kd , and T^k(I)=[2^k-1d , 2^kd]. The next iteration of T gives:

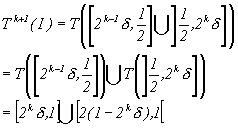
The next iteration gives that T ^k+2(I)=[0,2(1-2^kd)]È T([2(1-2^kd ),1[). Hence 1-2^kd <1/2 and there exists a number l, such that 2^l(1-2^kd )>1/2. The following therefore holds:

By the construction there exists a natural number k for every interval JÎ [0,1], such that T ^k(I)Ç J#Æ . Theorem 1.2. can now be used to finish the proof, since T(x) is continuous and topologically transitive on [0,1].

The baker map is chaotic on [0,1].

Proof: As for the tent map, it can be proved that B(x) is topologically transitive. B ⁿ(x) has 2 ⁿ fixed points, because the interval [0,1] consists of 2 ⁿ piecewise linear functions at the n:th iteration of B. Take now two n-periodical points, x and x', that are not separated by any other periodical points. The distance between these is now:

The periodical points are dense on [0,1]. The theorem 1.1. now gives that B(x) is chaotic on [0,1].

A perioddoubling occurs for the map f_l (x)=lx-(l+1)x³ at l=3.

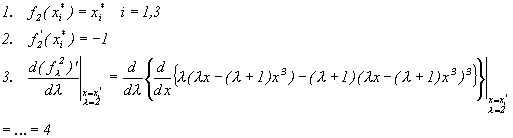
The cubic function f_l (x)=lx-(l+1)x³ is chaotic for l=3.

Consider . Put and h: S^1® [-1,1].

Now the following holds:

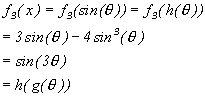
i.e. f ³(h(q ))=h(g(q )). Note that h is not a homeomorphism since it's a two-to-one at most points. The maps g and f₃ are semi-conjugate [Dev89]. Hence it is proved that g is chaotic. Example 1.1. shows that has dense periodical points on the unit circle. The map g is also topological transitive, because for any neighborhood U (in S¹) there exists k such that g ^k(U) covers S¹. Hence g is chaotic which also proves that f₃ is chaotic.