pH CONTROL

pH CONTROL

Tore Gustafsson

March 23, 1999

Introduction

The pH-control project at the Process Control Laboratory started back in 1975 with a 24-h record of the pH value of a wastewater tank of a chlorine plant. The record revealed an unstable control for one third of the day and a lazy control for the rest of the day.

Modeling and conventional control

The dynamics of stirred reactors with fast acid-base reactions was modeled by using the concept of reaction invariants [1], which resulted in general dynamic models for pH involving fast acid-base reactions [2]. Proper mathematical models for the dynamics of pH was earlier presented by Mellichamp et al. [3], in contrast to the ad hoc models which flourished at that time (and later) [4].

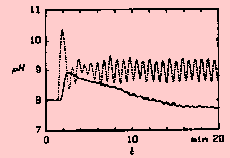
Figure 1. Measured pH in a pH control tank is oscillating about the set value at pH 9, while the measured pH value of a subsequent settling tank decreases towards 7.7 [5].

The model, together with experiments, revealed and explained the peculiarities experienced in pH control. One peculiarity is the following: In an oscillating pH-control loop the measured pH oscillates symmetrical around the set value, but when pH is measured from a subsequent damping tank the resulting pH might lie far outside the measured oscillations, see Figure 1 [5].

Some fundamentals in pH control [5], [6], [8]:

The extreme nonlinearity of the strong acid - strong base process does not exist in common industrial surroundings. All process water is buffered. E.g. distilled water in contact with air contains a considerable carbonic-acid buffer with a drastic reduction of nonlinearity compared to the unbuffered system.
The nonlinearity of a typical pH-control loop (feedback around a stirred tank) is not the main problem. The main problem is the severe performance demand (in terms of concentration) together with performance degrading components (esp. dead times) in the control loop.
Time-varying buffering is, however, a common source for poor pH control.

Adaptive control

The solution to time-varying buffering is adaptive control. Adaptive control can be

Adaptive control with linear feedback if we according to point two above do not consider nonlinearity to be a major problem.
Adaptive control with nonlinear feedback if we consider the richer model structure of a nonlinear model to have better prerequisites to adapt itself to the measured data.

Figure 2. Experimental adaptive nonlinear pH control of a system with severe variations in buffering [6], [7]. The experimental equipment consists of a controlled stirred tank with a subsequent settling tank. At k = 50 carbonate buffering is reduced to 1/6 of original concentration, at k = 300 buffering is restored to original level and at k = 700 carbonate concentration is reduced to zero mol/l. Additional load changes (strong base concentration) are introduced at additional time instants. Nomenclature: pH_f = pH of feed to the stirred tank, pH = controlled pH measured at the outlet of the stirred tank, u = normalized control signal, k = discrete time (sampling instant).

We have developed nonlinear adaptive control for pH, based on the general dynamic model for fast acid-base reactions [2], [7]. The adaptive controller is based on a nonlinear model for an acid-base system with fictitious acids. The fictitious acids are selected such that the model can give an accurate approximation of any fast acid-base system, or of a suitable subset of such fast acid-base systems. Popularly said, the controller adapts an approximate "titration curve" to a true "titration curve" of the system.
We have used an adaptive nonlinear model wich is linear in the adaptive parameters. This is obtained by using the concentrations of the "reaction invariant species" of the "reaction invariant" model [1] as adaptive parameters. Further we make some general assumptions on the flow properties. The reaction invariant model is continuously adapted online using a recursive least squares method. In a practical application proper methods for excitation of the system and forgetting of old data is essential for the performance and robustness of the controller.

This controller is compared to adaptive control with linear feedback in reference [7].

Slow acid-base reactions

Acid-base reactions between components in water solution are normally extremely fast, that is practically in equilibrium at any time. This is the normal presumption for dynamic models. The standard presumption is, however, not fulfilled if the reactions involve species, which are present in solid forms. This is in fact a common case. 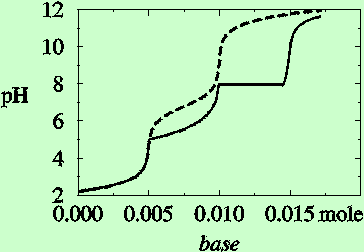The characteristics of a neutralization process can drastically be changed if solid salts are present [8]. A drastic example of the influence of precipitants is shown in Figure 3. A dynamic model must involve the speed of precipitation and dissolution, which, however, are not easy to characterize [8].

Figure 3. Titration curves for titration of 0.01 M H₃PO₄ with NaOH (dashed line) and with Ca(OH)₂ (solid line) [8]. Formation of solids deflect the titration curve in the latter case, giving a plateau at pH 8, where the pH of the solution does not change when base is added.

Fig.3. Titration curves of systems with/without solids.

Robust control

The dynamic model for slow acid-base reactions is a good testbench for multimodel robust control for nonlinear plants. A project on robust pH Control was done in co-operation with the project on Parametric Optimal Robust Control, giving a realistic object for implementation of robust multimodel control in a nonlinear process-environment [9].

The future

What is relevant in pH-control research? Many severe problems in pH control are solved by a careful choice of equipment (e.g. avoiding dead times) and conventional linear control. Systems with severe and fast variations in buffering might need adaptive control. A serious basis for adaptive control is the method developed in references [2] and [7]. This method is, however, developed for slowly changing buffering. In a system with fast variations in buffering this adaptive controller will start to oscillate. For general use the controller ought to be robustified in order to avoid oscillations, but it should also be made more robust for increasing buffering, that is able to swiftly react on decreasing process gains.

References

[1] Asbjørnsen, O.A., Reaction Invariants in the Control of Continuous Chemical Reactors, Chem. Engng Sci. 27 (1972), 709-717.

[2] Gustafsson, T.K. and K.V. Waller, Dynamic Modeling and Reaction Invariant Control of pH, Chem. Engng Sci. 38 (1983), 389-398.

[3] Mellichamp, D.A., D.R. Coughanowr and L.B. Koppel, Characterization and Gain Identification of Time Varying Flow Processes, AIChE J. 12 (1966), 75-82.

[4] Gustafsson, T.K., Calculation of the pH value of a mixture of solutions - an illustration of the use of chemical reaction invariants, Chem. Engng Sci. 37 (1982), 1419-1421.

[5] Waller, K.V. and T.K. Gustafsson, Fundamental Properties of pH Control, ISA Transactions 22 (1982), No. 1, 25-34.

[6] Gustafsson, T.K. and K.V. Waller, Nonlinear and Adaptive Control of pH, I&EC Research 31 (1992), 2681-2693.

[7] Gustafsson, T.K, An Experimental Study of a Class of Algorithms for Adaptive pH Control, Chem. Engng Sci. 40 (1985), 827-837.

[8] Gustafsson, T.K., B.O. Skrifvars, K.V. Sandström and K V. Waller, Modeling of pH for Control, I&EC Research 34 (1995), 820-827.

[9] Nyström, R.H., K.V. Sandström, T.K. Gustafsson and H.T. Toivonen, Multimodel Robust Control of Nonlinear Plants: A Case Study, J. Process Control 9 (1999), 135-150.

[Return to projects]